本文通过一个简单的例子，研究了低调制指数下调频（FM）和调相（PM）波的频谱。
正如我们从本系列的早期文章中所知，角度调制有两种形式：相位调制（PM）和频率调制（FM）。为了有效地传输和接收任何一种信号，了解调制波所占用的带宽至关重要。我们将具有低调制指数的角度调制波称为“窄带”。’
在这篇文章中，我们将通过探索这些窄带信号产生的频谱来推进我们对角度调制的讨论。在此过程中，我们将介绍一些概念，这些概念不仅是理解FM和PM波带宽要求的基础，也是分析某些RF电路线性性能的基础。
角度调制信号综述
恒定振幅、角度调制信号由以下方程表示：
方程式1其中：
Ac是载波振幅
fc是载波频率
ϕ（t）是相位偏差。
方程式2说明了PM方案中ϕ（t）与消息信号之间的关系：
方程式2其中m（t）是消息信号，kp是调制指数。
方程式3对FM方案也是如此：
方程式3鉴于消息信号是正弦函数的自变量，很明显调制波对消息信号的依赖是非线性的。
窄带角度调制波
我们之前将“窄带”定义为低调制指数。更确切地说，该术语适用于|ϕ（t）|远小于1弧度的特殊情况。为了推导窄带角度调制波的方程，我们首先通过应用基本三角恒等式来展开方程
方程式4如果|ϕ（t）|远小于1弧度，我们可以使用以下近似值：
方程式5调用这些近似值，方程式4简化为：
方程式6该表达式类似于传统幅度调制（AM）的方程，如下所示：
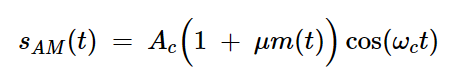方程式7在窄带角度调制波和传统AM中，同相分量都包含大量未调制载波。对于AM，同相分量还包括消息信息。对于窄带角度调制信号，消息信息包含在正交分量中。
为了确定角度调制波的频谱，我们将傅里叶变换应用于方程6，得到：
方程式8如果你很难推导出前面的方程，请记住正弦函数可以写成：
方程式9此外，傅里叶变换的频移特性表明，如果X（f）是X（t）的傅里叶变换，则我们有：
方程式10使用方程式9和10，您可以很容易地推导出窄带角度调制波的输出频谱。然而，在本文的其余部分，我们将继续使用方程式8。
示例：比较窄带角度调制和AM光谱
为了了解窄带FM和PM波产生的频谱，让我们考虑图1（a）中的消息信号频谱。该频谱对应于时域中的sinc函数。
正弦消息信号（a）和相应的传统AM波（b）的频谱。
图1 正弦消息信号（a）和相应的传统AM波（b）的频谱将方程7应用于该消息信号会产生传统的AM波，其频谱如图1（b）所示。接下来，让我们找到窄带PM和FM方案生成的光谱。
窄带PM光谱
图2（b）显示了与图1（a）的消息信号相对应的PM波的频谱。根据方程式2，ϕ（t）的光谱如图2（a）所示。
PM方案的相位偏差频谱（a）和相位调制波频谱（b）。
图2 PM方案（a）的ϕ（t）频谱和sinc消息信号（b）的PM波频谱将图2（b）与图1（b）进行比较，我们观察到这两个频谱在±fc处都具有冲激函数，并且包含消息频谱的副本。然而，对于大于零的频率，窄带PM频谱乘以系数j，对于f<0的频率，乘以–j。
系数±j表示相对于载波频率的90度相移。载波具有实值，因为它包含在方程6的同相分量中。相比之下，消息信息具有复杂的值，因为它位于正交分量中。
图3中的3D图提供了图2（b）中光谱的更准确表示。
PM波频谱的3D表示。
图3 示例PM波频谱的3D表示窄带调频频谱
为了找到窄带FM光谱，我们首先通过对方程3应用傅里叶变换来确定ϕ（t）的光谱。利用傅里叶变换的积分性质，我们得到：
方程式11请注意，函数积分的傅里叶变换会生成脉冲函数。为了简单起见，在上述方程中忽略了该脉冲函数。
图4显示了根据方程式11从M（f）推导Φ（f）的过程。
图4 FM波频域频谱的3D图示图4 FM方案的Φ（f）频谱，如3D所示。由于积分，Φ（f）的谱在虚平面内呈截断双曲线的形式。当应用窄带角度调制方程时，该虚分量乘以因子Ac/2j，将其转换回实分量。然后，我们得到图5（b）所示的窄带调频频谱。
FM方案的相位偏差频谱（a）和窄带FM波本身的频谱（b）。
图5 FM方案（a）的ϕ（t）频谱和窄带FM波（b）的频谱因为当应用窄带FM方程时，Φ（f）的虚分量会恢复为实分量，所以我使用2D图来表示最终的频谱。
窄带角度调制波的带宽
在上述示例中，窄带PM和FM方案占用2B的带宽，其中B是消息带宽。让我们看看我们是否可以利用这一点得出一些关于窄带角度调制信号带宽的一般结论。
我们知道窄带角度调制在载波频率附近产生Φ（f）的复制品（可能有实数或虚数缩放因子）。因此，调制信号的带宽等于Φ（f）带宽的两倍。但是Φ（f）的带宽与消息信号的带宽有什么关系呢？
对于PM，我们知道Φ（f）的带宽与消息信号的带宽相同（见方程式2）。另一方面，对于FM，ϕ（t）是通过对消息信号进行积分得到的（方程式3）。积分使时域信号平滑，或者换句话说，衰减其高频。因此，Φ（f）的带宽等于或小于消息信号的带宽。
由于ϕ（t）的最大带宽为B，我们可以得出结论，窄带角度调制信号的最大带宽是2B。这与双边带AM方案的最大带宽相同。
窄带角度调制信号产生电路
方程6的一个重要含义是，它提出了一种通过使用模拟乘法器和加法器来生成窄带角度调制波的方法。该电路的框图如图6所示。
用于生成窄带角度调制信号的电路框图。
图6 用于生成窄带角度调制信号的电路框图在未来的文章中，我们将看到上述电路是生成宽带角度调制信号的基本构建块。这是通过一种称为窄带到宽带转换的过程来实现的。
总结
角度调制，包括相位和频率调制，在通信系统中起着至关重要的作用，也是分析振荡器和频率合成器等电路的关键。在这篇文章中，我们考虑了一个简单的消息频谱，以深入了解窄带角度调制产生的频谱。正如我们所了解到的，这些频谱接近消息带宽的两倍。在下一篇文章中，我们将通过探索单频消息信号的窄带调制来继续讨论。
<!-- 非定向300*250按钮 17/09 wenjing begin --> <!-- 非定向300*250按钮 end -->
</div>
