你有没有过这样的经历?打开导航软件走路,明明站着没动,定位点却在屏幕上“漂移”;戴运动手表测心率,偶尔会跳出一个离谱的数值;甚至用体重秤,换个站姿数字就差了两斤。
这些“不靠谱”的情况,本质上都是同一个问题:传感器数据总会“说谎”。而卡尔曼滤波,就是专门给数据“打假”的技术——它像一位精明的侦探,从杂乱的信息中筛选出真相,让数据变得靠谱起来。
今天我们不用复杂公式,就用快递员送货的故事,把卡尔曼滤波讲明白。
一、先搞懂:为什么数据会“偏离”?
在说卡尔曼滤波之前,得先明白数据“偏离”的两个根源,这也是卡尔曼滤波要解决的核心问题:
1. 测量噪声:传感器的“手抖”
你用尺子量桌子,再小心也会有毫米级误差;IMU传感器测加速度,电子元件的微小波动就会让数值跳变。这种随机的、无规律的误差,就像传感器在“手抖”,我们叫它“测量噪声”。
2. 系统误差:模型的“预判偏差”
导航软件会根据你的速度预判下一秒位置,但如果突然刮阵风让你减速,预判就会不准;快递车按规划路线该到小区门口了,却因为堵车晚了5分钟——这种基于经验的“预判偏差”,就是系统误差。
卡尔曼滤波的核心思路特别简单:把“传感器的测量值”和“系统的预估值”结合起来,取一个最靠谱的中间值。就像你既听导航的路线建议,也看路边的路牌,两者结合才不会走错。
二、用快递员故事理解卡尔曼滤波的5步逻辑
假设快递员小K要给你送快递,我们需要实时定位他的位置。这时候有两个信息来源:
一是快递APP的“系统预判”(根据他的行驶速度算出来的位置)
二是他手机GPS的“测量值”(可能有漂移)。
卡尔曼滤波的思想其实很简单,就是 不断进行“预测”和“修正”:
预测:基于之前的数据,估算当前的值。
修正:用传感器或测量数据,对预测值进行调整,使其更加准确。
重复上述步骤,不断优化,使误差越来越小。
卡尔曼滤波就是这么工作的:
第1步:先猜一个“预估值”——我觉得你大概在这
快递APP知道小K10分钟前在A点,行驶速度是30km/h,方向是朝你家。按照这个信息推算,现在他应该到B点了——这就是“系统预估值”,专业说法叫“先验估计”。
但光有预判不够,得知道这个预判有多靠谱。如果小K走的是畅通的主干道,预判就准;如果是拥堵的老街区,预判误差就大——这个“靠谱程度”,卡尔曼滤波会用一个叫“协方差”的指标来量化,你不用记这个词,知道是“可信度评分”就行。
第2步:再拿一个“测量值”——GPS说你在这
同时,小K的手机GPS传来信号,显示他现在在C点。但我们知道GPS不是100%准,尤其是在高楼多的地方,可能会偏差几十米——这就是“测量值”。
和预判一样,测量值也有“可信度评分”:晴天开阔地,GPS可信度高;阴天高楼区,可信度低。
第3步:算“信任权重”——该信预判多一点,还是测量多一点?
这是卡尔曼滤波最关键的一步:谁的可信度高,就多听谁的。
比如:
如果小K在高速上(预判准,可信度90%),GPS又因为云层有点飘(可信度50%)——那最终位置就更靠近预判的B点。
如果小K在老街区(预判不准,可信度30%),GPS在开阔路口信号好(可信度90%)——那最终位置就更靠近测量的C点。
这个“信任权重”,就是卡尔曼滤波里的核心概念“卡尔曼增益”。简单说,就是“用两个数据的可信度,算出一个加权比例”。
第4步:出“最优值”——综合一下,你应该在这
根据算好的权重,把“预判值”和“测量值”结合起来,就能得到一个最靠谱的位置D点——这就是“后验估计”,也是我们最终用的定位结果。
举个具体数字:预判B点在坐标(100,200),测量C点在(105,203)。算出来权重是“预判占60%,测量占40%”,那最优位置就是(100×60%+105×40%, 200×60%+203×40%)=(102, 201.2),既修正了GPS的漂移,也弥补了预判的误差。
第5步:更新“经验”——为下一次预判做准备
最后一步很重要:用这次算出的最优值,更新系统的“经验库”。比如,发现小K实际行驶速度比预判慢了5km/h,那下一次预判时就会把这个误差考虑进去,让后续的预判越来越准。
这就是卡尔曼滤波的“闭环逻辑”——每一次计算都在修正过去的偏差,让下一次更精准。
三、不是消除误差,而是“管理”误差
看到这你可能会问:卡尔曼滤波能把误差完全去掉吗?答案是不能。但它的厉害之处在于,能在误差不可避免的情况下,找到“最优解”。
它就像一位经验丰富的老司机:
仪表盘速度表(测量值)偶尔跳变,他会结合自己的驾驶感受(系统预判),知道真实速度大概是多少;
遇到突发情况(大的测量误差),他不会完全相信仪表盘,也不会只靠感觉,而是两者结合做出判断。
这种“在不确定中找确定”的能力,让卡尔曼滤波成了工程领域的“万金油”。
下面结合实际,来简单的讲述卡尔曼滤波的公式:
假设一个汽车:
当前在 5 米的位置。
速度是 2 米/秒。
你想预测它 1 秒后的位置。
那么:预测位置=5+2=7 米
这就是卡尔曼滤波的预测阶段:
状态转移矩阵,描述状态如何从上一个时刻 k−1 变化到当前时刻 k。(例如速度的影响)可以把状态转移矩阵 A理解为一个“时间推进器”,它决定了当前状态如何变化到下一时刻。表示:1. 新位置 = 旧位置 + 速度 × 时间 2. 速度保持不变
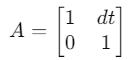
控制输入对状态的影响程度(控制矩阵)
控制输入(Control Input),表示 外部施加的影响,例如 加速、刹车、方向调整等(加速度)。如果没有外部输入,B 这部分可以忽略。
以上就是你预测汽车位置的一个过程,这在卡尔曼滤波中被定义为:预测阶段(Prediction Step),但是现实世界并不是完美的,测量数据会受到噪声影响,所以就还有接下来的过程,被称作修正阶段(Correction Step)如果你用测距仪器(有误差)发现汽车的位置是 6.5 米,而预测是 7 米,你会怎么办?
你不会完全相信预测值(速度或者位置是有一定偏差的 不是确定的5米初始位置和确定的2米/s的速度),也不会完全相信测量值(因为测量值也有误差),而是取一个折中值!取折中值的方式就是其实就是取一个权重。
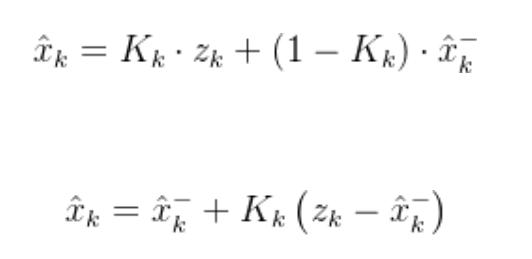

——卡尔曼增益,决定如何在预测和测量之间取折中。其实就相当于一个权重:如果测量值很可靠(传感器误差很小),那么取较大值,我们更相信测量值。如果测量值噪声较大,那么取较小值,我们更依赖预测值。
比如我们让=0.75(假设我们认为传感器测量较准确,但也不是说非常非常非常准)
按照公式:汽车真实的位置=0.75⋅6.5+0.25⋅7=6.625 米
上面就是最简单的卡尔曼滤波的过程。
四、原来它无处不在
别以为卡尔曼滤波只存在于实验室,它早就渗透到我们的日常生活中:
1. 导航定位:让你的高德/百度地图不“漂移”
手机导航时,卡尔曼滤波会同时处理GPS信号(测量值)、手机陀螺仪/加速度计数据(系统预判)、路网信息(辅助修正)。哪怕GPS信号暂时中断,它也能根据你之前的行驶状态,精准预判你的位置,不会让定位点“飞起来”。
2. 运动健康:让你的手环数据更靠谱
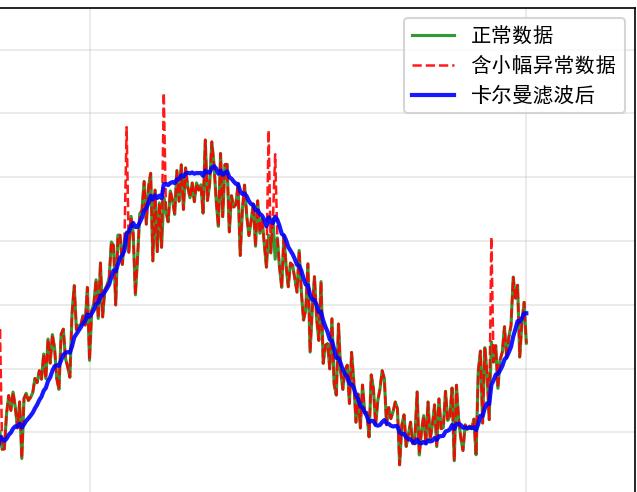
智能手环测心率时,偶尔会因为你抬手、出汗出现异常值(比如突然跳到150)。卡尔曼滤波会识别这种“突变”是噪声,结合你之前的心率趋势(比如一直在80左右),把异常值修正为合理范围,让你的运动数据更真实。
3. 自动驾驶:帮汽车“看清”路况
自动驾驶汽车的激光雷达、摄像头、毫米波雷达会产生大量数据。卡尔曼滤波会融合这些传感器的信息:比如摄像头看到“前方有障碍物”(测量值),结合汽车的行驶速度和方向(系统预判),排除摄像头因光影产生的误判,精准识别障碍物位置。
4. 无人机/机器人
无人机飞行时,IMU传感器会不断传回姿态数据(角度、加速度),但这些数据有噪声,容易导致无人机晃动。卡尔曼滤波会修正这些噪声,让无人机的姿态控制更平稳,不会因为一点数据波动就“失控”。
<!-- 非定向300*250按钮 17/09 wenjing begin --> <!-- 非定向300*250按钮 end -->
</div>

