编辑|杨文
你的童年我的童年好像不一样。
我的 17 岁,是坐在教室里苦哈哈地刷数学卷子;而这个名叫 Enrique Barschkis 的高中生,利用课间休息时间,成功解决了困扰数学家多年的埃尔德什第 347 号问题。

这一成就不仅在社交平台 X 上引发热议,更得到了谷歌首席科学家 Jeff Dean 的盛赞。
什么是埃尔德什第 347 号问题?
埃尔德什第 347 号问题,最初由埃尔德什和格雷厄姆在 1980 年提出,核心问题是:是否存在一个整数序列,其中相邻项的比值趋近于 2,并且对于该序列的任何余有限子序列,其有限子集和构成的集合在自然数中的密度都是 1?
这个问题触及了数论中完全序列理论的核心,其难度在于需要在严格的增长率限制下,保证几乎所有足够大的正整数都能表示为序列中某些项的和。

去年 10 月,著名数学家、菲尔兹奖得主陶哲轩在 Erdős 问题网站的讨论区里,用 ChatGPT 搜索相关文献,找到了一篇 Burr 和 Erdős 的旧论文。

然而数学家沃特很快发现,那篇论文中的结果使用的是相邻两项的比值条件,与本问题要求的相邻项比值条件略有不同。

陶哲轩提出了一个巧妙的构造思路:将序列分成若干个区块,每个区块长度缓慢增长,通过精心设计每个区块内的元素比例和区块之间的连接,使得序列既满足比值趋近于 2 的要求,又能保证其子集和覆盖几乎所有自然数。这个想法基于一种类似进位制的表示方法,通过在每个区块末尾添加调整项,为数的表示提供足够的灵活性。

17 岁少年完成完整证明
这个构想在讨论区挂了三个月,直到 2026 年 1 月 21 日晚上,这个 17 岁的高中生 Enrique 发帖宣布:他完成了完整的证明。
他在陶哲轩和沃特的思路基础上,构造了一个具体的序列:将序列分成若干区块,第 n 个区块的长度大约是对数的对数级别增长,区块内部由几何级数构成,区块之间通过精心设计的调整项连接。这种构造确保了相邻项比值在整体上趋近于 2,同时通过「进位调整」机制,使得几乎所有正整数都能表示为序列中某些项的和。

他还使用人工智能工具 Aristotle 将这个证明完全形式化为 Lean 语言代码,这是数学证明可以被计算机严格验证的形式。
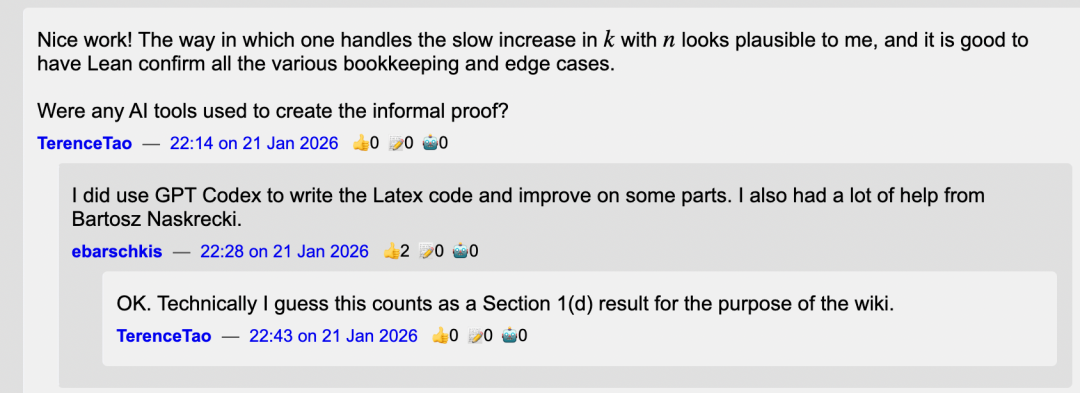
陶哲轩在看到 Enrique 的证明后评论道:「干得漂亮!你处理 k 随 n 缓慢增长的方式在我看来是合理的,而且很高兴看到 Lean 确认了所有各种簿记和边界情况。」
他随即询问:「创建非形式证明时使用了 AI 工具吗?」Enrique 坦诚地回答,他使用了 GPT Codex 来编写 LaTeX 代码并改进部分内容,同时得到了数学家 Bartosz Naskręcki 的大量帮助。
Bartosz Naskręcki 随后转发并评论:「Enrique 几周前给我发邮件,随意聊了聊椭圆曲线离散对数问题。我们用模型和 Aristotle 测试了他的许多想法。我为他感到非常自豪,在高中课间休息的间隙,他在 17 岁时就开辟了通往数学前沿的道路!我的建议只包含适度的提示和鼓励。Enrique 理应获得全部荣誉,他的勇气和热情值得赞扬。好运,伙计 —— 向星辰进发!」

谷歌的 Jeff Dean 也转发了这条消息:「爱看这种事,17 岁的 Enrique 解决了一个有趣的数学问题,与陶哲轩讨论,并感谢 Bartosz Naskręcki 给予的 『 大量帮助 』 ,而 Bartosz 说他实际上提供的帮助很少。这种广泛分享荣誉的本能真是太棒了!」

目前 Erdős Problems 网站已经将问题 #347 标记为「肯定解决」,这意味着 Enrique 的解决方案得到了数学社区的认可。
这件事的意义远不止一个少年解决了一道难题那么简单。它标志着数学研究正在进入一个新阶段:年轻研究者借助 AI 工具,能够更快地触及学科前沿。
随着 AI 工具的不断进步,类似的突破可能会越来越多。未来的数学研究,或许将是人类创造力与人工智能计算力深度融合。
https://x.com/JeffDean/status/2014195425277100251
https://www.erdosproblems.com/forum/thread/347
]article_adlist–>
]article_adlist–>
<!-- 非定向300*250按钮 17/09 wenjing begin --> <!-- 非定向300*250按钮 end -->
</div>

