<p><strong>线性变换</strong></p> x’=Ax,其中A是矩阵,x’和x都是向量,这是一种原点不变,且原有的平行关系和倍数关系都不变的空间视角转换,它转换的是从不同空间视角来看x这个向量,x’和x其实是同一个向量,只不过所看的视角不同罢了。具体的内容可以参考线性代数整理(二) 中的线性变换。它是所有计算机图形学的基础。
仿射变换
仿射变换是在线性变换的基础上,原点可以发生变换。
x’=Ax+b,其中A是矩阵,x’、x、b都是向量。
仿射变换是单纯对图片进行平移、缩放、倾斜和旋转,而这几个操作都不会改变图片线之间的平行关系。如果用三维线性表达就是
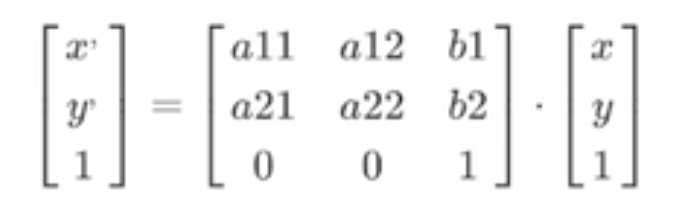
那么它又满足了线性变换的基本格式,具体实例可以参考OpenCV计算机视觉整理 中的图像的仿射变换。这里我们将不使用opencv内置方法,而使用numpy来重写第二个图形旋转实例,方便理解。
import numpy as np import math from PIL import Image import cv2 def affine_transform_numpy(image, transform_matrix): """ 使用 numpy 实现仿射变换 Args: image: 输入图像的 numpy 数组 (H, W, C) transform_matrix: 2x3 的仿射变换矩阵 Returns: 变换后的图像 numpy 数组 """ h, w, channels = image.shape # 创建输出图像 output = np.zeros_like(image) # 计算变换矩阵的逆矩阵(用于反向映射) # 将 2x3 矩阵扩展为完整的 3x3 矩阵,对应公式中的完整变换矩阵 : # [a11 a12 b1] # [a21 a22 b2] # [0 0 1 ] <- 齐次坐标的底行 full_matrix = np.vstack([transform_matrix, [0, 0, 1]]) print(" 完整的 3x3 变换矩阵 :") print(full_matrix) try: # 计算逆矩阵 - 用于反向映射 # 正向映射 : [x', y'] = M * [x, y] ( 从原图到目标图 ) # 反向映射 : [x, y] = M^(-1) * [x', y'] ( 从目标图回到原图 ) inv_matrix = np.linalg.inv(full_matrix) print(" 逆变换矩阵 :") print(inv_matrix) inv_transform = inv_matrix[:2, :] # 取前两行,得到 2x3 逆变换矩阵 print(" 用于反向映射的 2x3 矩阵 :") print(inv_transform) except np.linalg.LinAlgError: print(" 变换矩阵不可逆,返回原图像 ") return image # 创建目标图像的坐标网格 - 对应公式中的 [x', y', 1] y_coords, x_coords = np.mgrid[0:h, 0:w] # 将坐标转换为齐次坐标形式 [x', y', 1] ,每列是一个像素的坐标 coords = np.stack([x_coords.ravel(), y_coords.ravel(), np.ones(x_coords.size)]) print(" 目标图像坐标矩阵形状 :", coords.shape) print(" 前 5 个像素的齐次坐标 : \n ", coords[:, :5]) # 应用逆变换获取源图像坐标,跟原始公式不同,这里使用的是逆变换, @ 在 python 中是矩阵乘法 # [x, y, 1]^T = M^(-1) * [x', y', 1]^T source_coords = inv_transform @ coords source_x = source_coords[0].reshape(h, w) source_y = source_coords[1].reshape(h, w) # 双线性插值 for c in range(channels): output[:, :, c] = bilinear_interpolation(image[:, :, c], source_x, source_y) return output.astype(np.uint8) def bilinear_interpolation(image, x_coords, y_coords): """ 双线性插值 Args: image: 单通道图像 (H, W) x_coords: x 坐标数组 y_coords: y 坐标数组 Returns: 插值后的图像 """ h, w = image.shape output = np.zeros_like(x_coords) # 找到有效的坐标范围 valid_mask = (x_coords >= 0) & (x_coords < w - 1) & (y_coords >= 0) & (y_coords < h - 1) # 获取有效坐标 valid_x = x_coords[valid_mask] valid_y = y_coords[valid_mask] if len(valid_x) == 0: return output # 计算整数和小数部分 x0 = np.floor(valid_x).astype(int) y0 = np.floor(valid_y).astype(int) x1 = x0 + 1 y1 = y0 + 1 # 确保坐标在有效范围内 x1 = np.clip(x1, 0, w - 1) y1 = np.clip(y1, 0, h - 1) # 计算权重 dx = valid_x - x0 dy = valid_y - y0 # 双线性插值 # I(x,y) = I(x0,y0)(1-dx)(1-dy) + I(x1,y0)dx(1-dy) + I(x0,y1)(1-dx)dy + I(x1,y1)dxdy interpolated = (image[y0, x0] * (1 - dx) * (1 - dy) + image[y0, x1] * dx * (1 - dy) + image[y1, x0] * (1 - dx) * dy + image[y1, x1] * dx * dy) output[valid_mask] = interpolated return output def create_rotation_matrix(theta): """ 创建旋转变换矩阵 Args: theta: 旋转角度(弧度) Returns: 2x3 的旋转矩阵 """ cos_theta = math.cos(theta) sin_theta = math.sin(theta) # 对应公式中的 2x3 变换矩阵 : # [a11 a12 b1] [cos(θ) sin(θ) 0] # [a21 a22 b2] = [-sin(θ) cos(θ) 0] # 这是纯旋转矩阵,没有平移分量 (b1=0, b2=0) rotation_matrix = np.array([ [cos_theta, sin_theta, 0], # [a11, a12, b1] [-sin_theta, cos_theta, 0] # [a21, a22, b2] ], dtype=np.float32) return rotation_matrix def create_translation_matrix(tx, ty): """ 创建平移变换矩阵 Args: tx: x 方向平移量 ty: y 方向平移量 Returns: 2x3 的平移矩阵 """ translation_matrix = np.array([ [1, 0, tx], [0, 1, ty] ], dtype=np.float32) return translation_matrix if __name__ == "__main__": try: # 使用 PIL 读取图像 pil_image = Image.open("/Users/admin/Documents/111.jpeg") # 转换为 numpy 数组 img = np.array(pil_image) if len(img.shape) == 3: h, w, ch = img.shape else: # 如果是灰度图像,添加通道维度 img = np.expand_dims(img, axis=2) h, w, ch = img.shape print(f" 图像尺寸 : {h} x {w} x {ch} ") # 创建旋转变换矩阵(逆时针旋转 15 度) theta = math.pi / 12 # 15 度 rotation_matrix = create_rotation_matrix(theta) # 可以组合多个变换,例如先旋转再平移 # translation_matrix = create_translation_matrix(100, 100) # combined_matrix = translation_matrix @ np.vstack([rotation_matrix, [0, 0, 1]]) # transform_matrix = combined_matrix[:2, :] # 旋转矩阵是 2*2 的,这里没有平移,故变换矩阵只有旋转矩阵 transform_matrix = rotation_matrix print(" 变换矩阵 :") print(transform_matrix) # 应用仿射变换 print(" 正在进行仿射变换 ...") transformed_img = affine_transform_numpy(img, transform_matrix) # 转换图像格式用于 opencv 显示 (RGB -> BGR) if ch == 3: img_bgr = cv2.cvtColor(img, cv2.COLOR_RGB2BGR) transformed_img_bgr = cv2.cvtColor(transformed_img, cv2.COLOR_RGB2BGR) else: img_bgr = img transformed_img_bgr = transformed_img # 使用 opencv 显示图像 cv2.namedWindow('Original Image', cv2.WINDOW_NORMAL) cv2.namedWindow('Transformed Image', cv2.WINDOW_NORMAL) cv2.imshow('Original Image', img_bgr) cv2.imshow('Transformed Image', transformed_img_bgr) print(" 按任意键关闭窗口 ...") cv2.waitKey(0) cv2.destroyAllWindows() # 保存变换后的图像 output_pil = Image.fromarray(transformed_img) output_path = "/Users/admin/Documents/111_transformed.jpeg" output_pil.save(output_path) print(f" 变换后的图像已保存到 : {output_path} ") except FileNotFoundError: print(" 错误 : 找不到图像文件 /Users/admin/Documents/111.jpeg") print(" 请确保图像文件存在,或修改文件路径 ") except Exception as e: print(f" 处理图像时发生错误 : {e} ")
这是反向映射的代码,对于完全满足公式的正向映射代码如下
import numpy as np import math from PIL import Image import cv2 def affine_transform_numpy(image, transform_matrix, fill_holes=True): """ 使用 numpy 实现仿射变换(正向映射,优化版) Args: image: 输入图像的 numpy 数组 (H, W, C) transform_matrix: 2x3 的仿射变换矩阵 fill_holes: 是否填充空洞,默认 True Returns: 变换后的图像 numpy 数组 """ h, w, channels = image.shape # 创建输出图像 output = np.zeros_like(image) # 正向映射:使用原始变换矩阵,完全按照数学公式 # [x', y'] = M * [x, y] ( 从原图到目标图 ) print(" 正向映射变换矩阵 (2x3):") print(transform_matrix) # 优化坐标计算:直接创建坐标矩阵 print(" 创建坐标网格 ...") y_indices, x_indices = np.mgrid[0:h, 0:w] # 创建齐次坐标矩阵 (3, h*w) coords = np.vstack([ x_indices.ravel(), y_indices.ravel(), np.ones(h * w, dtype=np.float32) ]) print(" 原图像坐标矩阵形状 :", coords.shape) print(" 前 5 个像素的齐次坐标 : \n ", coords[:, :5]) # 应用正向变换获取目标图像坐标,完全按照原始公式, @ 在 python 中是矩阵乘法 # [x', y']^T = M * [x, y, 1]^T print(" 计算变换后坐标 ...") target_coords = transform_matrix @ coords target_x = target_coords[0].reshape(h, w) target_y = target_coords[1].reshape(h, w) print(" 变换后坐标范围 :") print(f"x': [ {np.min(target_x): .2f } , {np.max(target_x): .2f } ]") print(f"y': [ {np.min(target_y): .2f } , {np.max(target_y): .2f } ]") # 正向映射:使用向量化操作,大幅提升性能 print(" 使用向量化操作进行正向映射 ...") # 向量化处理:找到所有有效的目标坐标 valid_mask = ((target_x >= 0) & (target_x < w) & (target_y >= 0) & (target_y < h)) # 获取有效的坐标 valid_target_x = target_x[valid_mask] valid_target_y = target_y[valid_mask] # 四舍五入到整数坐标 target_x_int = np.round(valid_target_x).astype(int) target_y_int = np.round(valid_target_y).astype(int) # 确保坐标在边界内(向量化 clip 操作) target_x_int = np.clip(target_x_int, 0, w - 1) target_y_int = np.clip(target_y_int, 0, h - 1) # 获取对应的原图像坐标 y_coords_flat = np.repeat(np.arange(h), w) x_coords_flat = np.tile(np.arange(w), h) valid_y_orig = y_coords_flat[valid_mask.ravel()] valid_x_orig = x_coords_flat[valid_mask.ravel()] # 向量化复制像素值 if channels == 1: output[target_y_int, target_x_int] = image[valid_y_orig, valid_x_orig] else: for c in range(channels): output[target_y_int, target_x_int, c] = image[valid_y_orig, valid_x_orig, c] # 可选的后处理:填补空洞 if fill_holes: output = fill_holes_simple(output) print(f" 变换完成!有效像素比例 : {np.sum(output > 0) / output.size * 100 : .2f } %") return output.astype(np.uint8) def fill_holes_simple(image): """ 优化的空洞填充算法(向量化实现) 使用邻域平均值填充空洞(像素值为 0 的位置) Args: image: 包含空洞的图像 Returns: 填充后的图像 """ if np.all(image != 0): return image # 没有空洞,直接返回 print(" 正在填充空洞 ...") output = image.copy() h, w = image.shape[:2] # 使用卷积进行快速邻域填充 from scipy import ndimage if len(image.shape) == 3: channels = image.shape[2] for c in range(channels): channel = image[:, :, c] # 找到空洞位置 holes = (channel == 0) if np.any(holes): # 使用均值滤波填充 # 创建权重矩阵(忽略 0 值) weights = (channel > 0).astype(float) # 计算加权平均 kernel = np.ones((3, 3)) sum_values = ndimage.convolve(channel.astype(float), kernel, mode='constant') sum_weights = ndimage.convolve(weights, kernel, mode='constant') # 避免除以 0 valid_weights = sum_weights > 0 filled_values = np.zeros_like(sum_values) filled_values[valid_weights] = sum_values[valid_weights] / sum_weights[valid_weights] # 只在空洞位置填充 output[holes, c] = filled_values[holes] else: # 灰度图像 holes = (image == 0) if np.any(holes): weights = (image > 0).astype(float) kernel = np.ones((3, 3)) sum_values = ndimage.convolve(image.astype(float), kernel, mode='constant') sum_weights = ndimage.convolve(weights, kernel, mode='constant') valid_weights = sum_weights > 0 filled_values = np.zeros_like(sum_values) filled_values[valid_weights] = sum_values[valid_weights] / sum_weights[valid_weights] output[holes] = filled_values[holes] return output def bilinear_interpolation(image, x_coords, y_coords): """ 双线性插值 Args: image: 单通道图像 (H, W) x_coords: x 坐标数组 y_coords: y 坐标数组 Returns: 插值后的图像 """ h, w = image.shape output = np.zeros_like(x_coords) # 找到有效的坐标范围 valid_mask = (x_coords >= 0) & (x_coords < w - 1) & (y_coords >= 0) & (y_coords < h - 1) # 获取有效坐标 valid_x = x_coords[valid_mask] valid_y = y_coords[valid_mask] if len(valid_x) == 0: return output # 计算整数和小数部分 x0 = np.floor(valid_x).astype(int) y0 = np.floor(valid_y).astype(int) x1 = x0 + 1 y1 = y0 + 1 # 确保坐标在有效范围内 x1 = np.clip(x1, 0, w - 1) y1 = np.clip(y1, 0, h - 1) # 计算权重 dx = valid_x - x0 dy = valid_y - y0 # 双线性插值 # I(x,y) = I(x0,y0)(1-dx)(1-dy) + I(x1,y0)dx(1-dy) + I(x0,y1)(1-dx)dy + I(x1,y1)dxdy interpolated = (image[y0, x0] * (1 - dx) * (1 - dy) + image[y0, x1] * dx * (1 - dy) + image[y1, x0] * (1 - dx) * dy + image[y1, x1] * dx * dy) output[valid_mask] = interpolated return output def create_rotation_matrix(theta): """ 创建旋转变换矩阵 Args: theta: 旋转角度(弧度) Returns: 2x3 的旋转矩阵 """ cos_theta = math.cos(theta) sin_theta = math.sin(theta) # 对应公式中的 2x3 变换矩阵 : # [a11 a12 b1] [cos(θ) sin(θ) 0] # [a21 a22 b2] = [-sin(θ) cos(θ) 0] # 这是纯旋转矩阵,没有平移分量 (b1=0, b2=0) rotation_matrix = np.array([ [cos_theta, sin_theta, 0], # [a11, a12, b1] [-sin_theta, cos_theta, 0] # [a21, a22, b2] ], dtype=np.float32) return rotation_matrix def create_translation_matrix(tx, ty): """ 创建平移变换矩阵 Args: tx: x 方向平移量 ty: y 方向平移量 Returns: 2x3 的平移矩阵 """ translation_matrix = np.array([ [1, 0, tx], [0, 1, ty] ], dtype=np.float32) return translation_matrix if __name__ == "__main__": try: # 使用 PIL 读取图像 pil_image = Image.open("/Users/admin/Documents/111.jpeg") # 转换为 numpy 数组 img = np.array(pil_image) if len(img.shape) == 3: h, w, ch = img.shape else: # 如果是灰度图像,添加通道维度 img = np.expand_dims(img, axis=2) h, w, ch = img.shape print(f" 图像尺寸 : {h} x {w} x {ch} ") # 创建旋转变换矩阵(逆时针旋转 15 度) theta = math.pi / 12 # 15 度 rotation_matrix = create_rotation_matrix(theta) # 可以组合多个变换,例如先旋转再平移 # translation_matrix = create_translation_matrix(100, 100) # combined_matrix = translation_matrix @ np.vstack([rotation_matrix, [0, 0, 1]]) # transform_matrix = combined_matrix[:2, :] # 正向映射:直接使用 2x3 变换矩阵,按照数学公式 [x', y'] = M * [x, y, 1] transform_matrix = rotation_matrix print(" 变换矩阵 :") print(transform_matrix) # 应用仿射变换(正向映射) print(" 正在进行仿射变换(正向映射) ...") import time start_time = time.time() # 可以选择是否填充空洞(填充空洞会增加处理时间) fill_holes_option = True # 改为 False 可以跳过空洞填充,提升性能 transformed_img = affine_transform_numpy(img, transform_matrix, fill_holes=fill_holes_option) end_time = time.time() print(f" 变换耗时 : {end_time - start_time: .3f } 秒 ") # 转换图像格式用于 opencv 显示 (RGB -> BGR) if ch == 3: img_bgr = cv2.cvtColor(img, cv2.COLOR_RGB2BGR) transformed_img_bgr = cv2.cvtColor(transformed_img, cv2.COLOR_RGB2BGR) else: img_bgr = img transformed_img_bgr = transformed_img # 使用 opencv 显示图像 cv2.namedWindow('Original Image', cv2.WINDOW_NORMAL) cv2.namedWindow('Transformed Image', cv2.WINDOW_NORMAL) cv2.imshow('Original Image', img_bgr) cv2.imshow('Transformed Image', transformed_img_bgr) print(" 按任意键关闭窗口 ...") cv2.waitKey(0) cv2.destroyAllWindows() # 保存变换后的图像 output_pil = Image.fromarray(transformed_img) output_path = "/Users/admin/Documents/111_transformed.jpeg" output_pil.save(output_path) print(f" 变换后的图像已保存到 : {output_path} ") except FileNotFoundError: print(" 错误 : 找不到图像文件 /Users/admin/Documents/111.jpeg") print(" 请确保图像文件存在,或修改文件路径 ") except Exception as e: print(f" 处理图像时发生错误 : {e} ")
透视变换
仿射变换是在二维空间中的旋转、平移和缩放,透视变换是在三维空间中的视角变化。相对于仿射,透视变换能保持”直线性”,原图像中的直线,经透视变换后仍为直线。
如果说仿射变换是对三维空间中某个平面的一些二维变化,透视变换就是对这个平面进行变换,并且利用视觉原理对图像进行一定处理(近大、远小)。
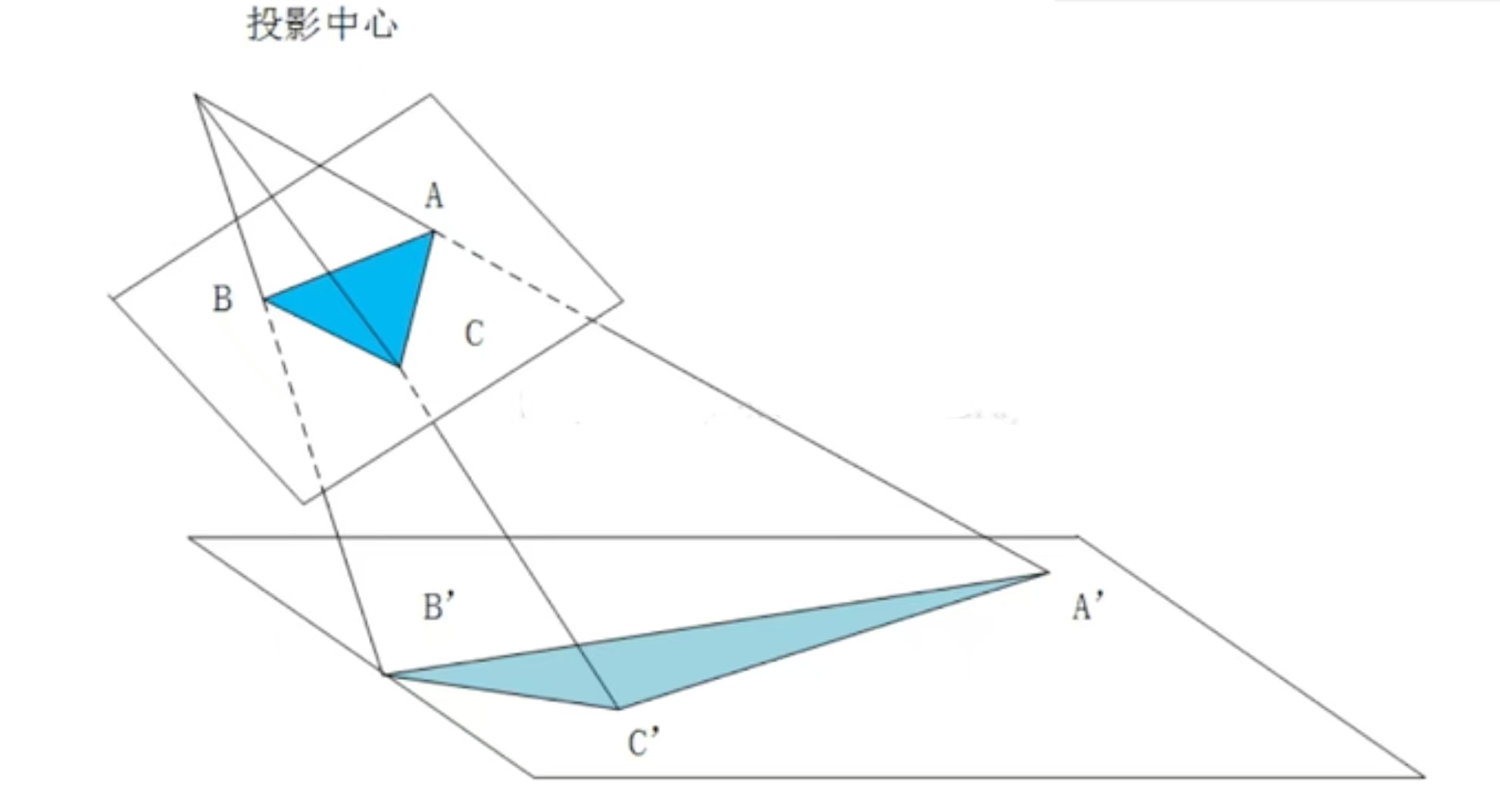
- 投影中心(Projection Center)
- 图中顶部标注的”投影中心”是透视变换的核心点
- 就像人的眼睛位置或相机镜头的光心
- 所有的投影线都从这个点发出
- 原始图形:三角形ABC
- 深蓝色三角形ABC是原始图形
- 位于较近的投影平面上
- 各个顶点坐标为A、B、C
- 变换后图形:三角形A’B’C’
- 浅蓝色三角形A’B’C’是透视变换的结果
- 位于较远的投影平面上
- 各个顶点坐标为A’、B’、C’
- 第一步:建立投影射线,从投影中心分别向原图形的每个顶点画射线:
- 投影中心 → A点:形成射线PA
- 投影中心 → B点:形成射线PB
- 投影中心 → C点:形成射线PC
- 第二步:确定目标投影平面,设定一个新的投影平面(图中下方的平面),这个平面通常:
- 平行于原平面,但距离投影中心更远
- 或者以某个角度倾斜
- 第三步:计算交点坐标,每条投影射线与目标平面的交点就是变换后的坐标:
- 射线PA与目标平面交于A’
- 射线PB与目标平面交于B’
- 射线PC与目标平面交于C’
- 第四步:形成变换结果
- 连接新的顶点A’、B’、C’,形成变换后的三角形
- 注意:形状发生了显著变化,不再是相似变换
- 非线性变换
- 直线仍保持直线(除了通过投影中心的直线)
- 角度不保持不变**
- 长度比例不保持不变**
- 面积比例不保持不变**
- 齐次坐标表示,透视变换使用齐次坐标:
- [x’] [h11 h12 h13] [x]
- [y’] = [h21 h22 h23] [y]
- [w’] [h31 h32 h33] [w]
- 最终坐标:x_final = x’/w’, y_final = y’/w’
- 近大远小效应
- 从图中可以看出,离投影中心近的物体(ABC)看起来较大
- 离投影中心远的物体(A’B’C’)看起来较小
- 这正是透视效果的本质
齐次坐标系与笛卡尔坐标系
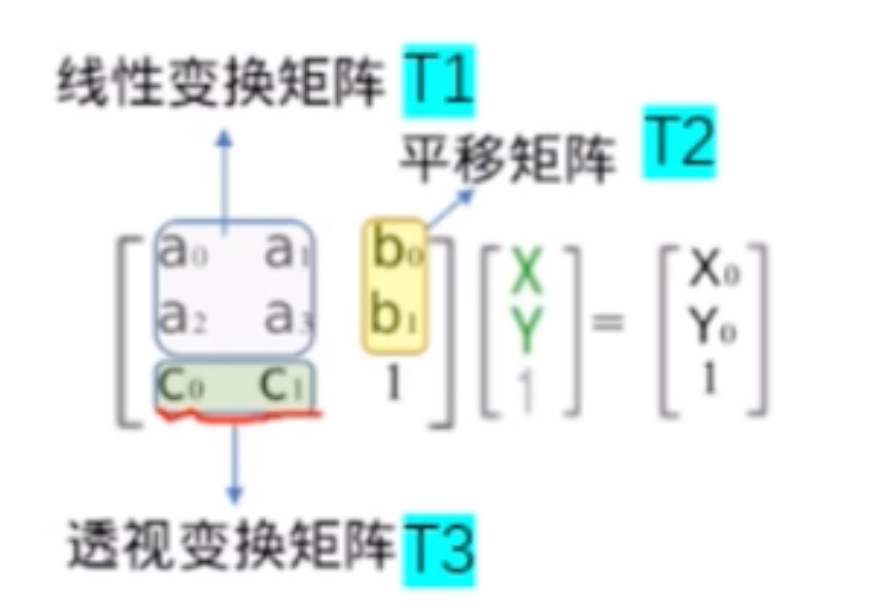
我们说透视变换是非线性变换,但是从上面的公式来看,在齐次坐标系中它满足线性变换的基本格式,但最终我们需要转换回笛卡尔坐标。
齐次坐标系
我们知道线性变换x’=Ax无法改变原点,即无法发生位移。但仿射变换x’=Ax+b可以,为什么我们要将这一加法操作转变为直接的矩阵乘法操作呢?
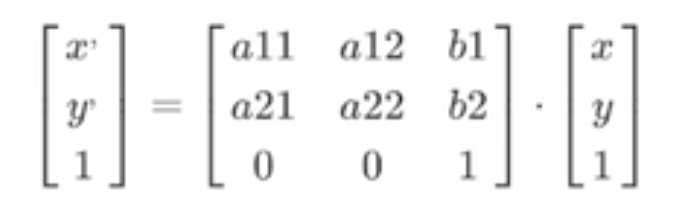
我们将平移值\([b_1 b_2]^T\),即向量b放在矩阵的右上角达到了相同的结果
- \(x’=a_{11}x+a_{12}y+b_1\)
- \(y’=a_{21}x+a_{22}y+b_2\)
- 1=1
这里的1=1很重要,我们知道对于平面上的运算,二维就够了,可为什么要用到三维坐标呢?这里就需要引入齐次坐标的概念。
齐次坐标是一种用n+1维来表示n维点的方法。简单来说,就是用额外的维度来表示点的”权重”或”深度”。它的好处就是可以使用矩阵乘法。
对于计算机来说,如果只使用二维的加法运算,对于一个图形有大量的点,计算耗时耗力,而矩阵乘法对于GPU来说,只需要一步完成。
而齐次坐标由\([x\ y\ 1]^T\)变成\([x\ y\ 0]^T\)时,其实就是没有平移的线性变换,原点不变。但其实齐次坐标为0时又表示平面内的无穷远点,我们知道只有二维坐标\([x\ y]^T\)时,无论x,y取何值,都无法表达∞这个概念,而\([x\ y\ 0]^T\)的齐次坐标则表达为无穷远点,它只表达方向。那既不是1又不是0时会怎样呢?如\([x\ y\ w]^T\),可以看作是3D空间中从原点出发的射线。在这种情况下,规则是要将恢复的的向量的每个分量除以齐次坐标w,以使齐次值回到1
\([\frac {x}{w}\ \frac {y}{w}\ 1]^T\)
那么这里的\(\frac {x}{w}\)和\(\frac {y}{w}\)就是笛卡尔坐标系中的坐标。齐次坐标w表示一个归一化的深度值,该值越大,投影后的物体越小;该值越小,投影后的物体越大。这里我们用透镜成像来理解就会更简单。
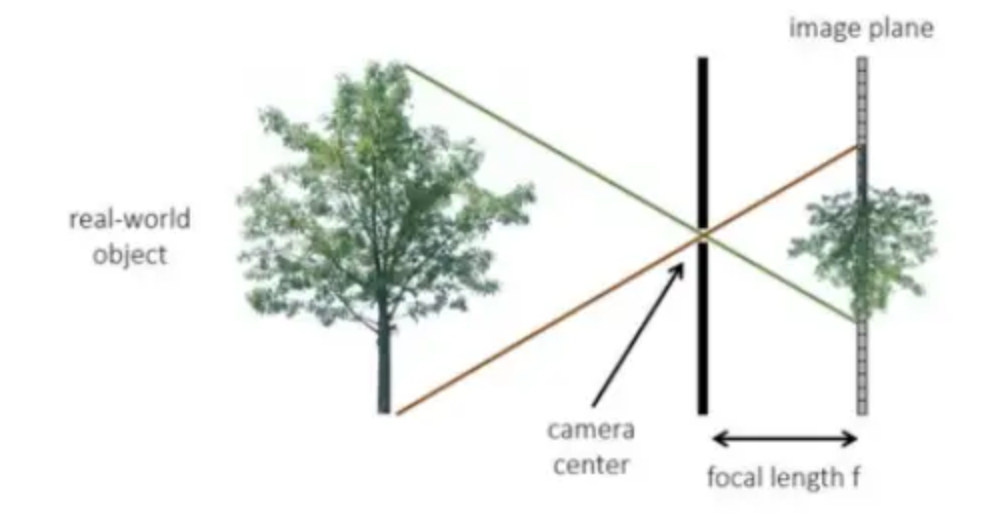
上图中,投影中心就是透镜的中心点,它到真实物体树的垂直距离为Z,它到后方投影平面的距离为焦距f,则\(w=\frac {Z}{f}\),在f固定不变的情况下,Z越大,w越大,在成像平面中,树的像就越小(这里需要注意的是树不是等比例放大的,它在任何位置都是同样大小的,越远的树的上下两端与原点的夹角就会越小,成像也会越小)。固定Z不变,f越小,w越大,在成像平面中,树也会越来越小。
笛卡尔坐标系
笛卡尔坐标系简单理解就是我们最常用的二维平面直角坐标系,也是仿射变换的基础。齐次坐标系就是一个三维空间坐标系,但是\([x\ y\ w]^T\)中的w并不表示一个距离坐标,它仅仅只是一个数学参数,代表权重;x,y是成像平面中的二维坐标。
</div>维权提醒:如果你或身边的朋友近五年内因投顾公司虚假宣传、诱导交费导致亏损,别放弃!立即联系小羊维权(158 2783 9931,微信同号),专业团队帮你讨回公道! 📞立即免费咨询退费



