使用三阶截距点(IP3)度量,我们研究了级联射频系统中单个增益级的非线性如何影响级联整体的线性性能。
本系列的早期文章探讨了评估射频组件线性度的关键概念,例如1 dB压缩点和三阶截距点(IP3)。在实践中,我们的系统由多个以级联方式连接的组件组成。最终,我们感兴趣的是整个系统的线性性能。
本文探讨了级联系统的线性度与构成级联的各个组件的线性度之间的关系。理解这种关系至关重要,因为它使我们能够识别限制系统线性的组件。
确定IM3组件的功率
当双音输入由⍵1和ᮥ2的频率分量组成时,三阶非线性会在输入频率附近产生失真分量。我们将使用术语IM3来指出现在2°1-°2和2°2-°1的带内互调分量。
考虑一个双音测试,其中每个输入音的功率为P1,dBm。如图1所示,本次测试的输出基波和IM3分量的功率分别为PF,dBm和PIM,dBm。
双音测量中输出基波和IM3分量的功率与输入功率的关系。
 图1 双音测量中输出基波和IM3分量的功率与输入功率的关系
图1 双音测量中输出基波和IM3分量的功率与输入功率的关系在本文的这一部分中,我们将制定一个方程来确定IM3组件的功率。稍后,我们将使用这个方程来评估级联系统的非线性。
假设施加的输入功率(P1,dBm)和输入三阶截距点(IIPdBm)之间的差为ΔP。由于IM3功率以3:1的斜率上升,输出截距点(OIPdBm)和PIM之间的差值dBm为3ΔP。此外,由于线性输出的斜率为1,OIPdBm和PF之间的差值dBm为ΔP。从上图可以看出,PF,dBm和PIM,dBm之间的差值为2ΔP:
 方程式1
方程式1将OIPdBm–PF,dBm=ΔP代入上述方程,我们得到:
 方程式2
方程式2其简化为:
 方程式3
方程式3在上述分析中,功率量以分贝为单位。方程式3的线性等价物为:
 方程式4
方程式4方程4以线性形式给出了功率量,是本文的基石。该方程表明,IM3组件的功率与基波输出功率的立方成正比,与电路输出IP3点的平方成反比。稍后,我们将使用它来确定IM3组件在级联不同节点上的功率。不过,在此之前,我们需要研究IM3组件的产生机制。
级联系统中的IM3生成
考虑一个无记忆非线性阶段,其输入输出特性由三次多项式表达式近似表示:
 方程式5
方程式5如果我们对上述电路应用双音输入,输出端会出现几个不同的谐波和非谐波(即互调)分量。图2显示了双音测试中生成的输出频率分量。
当输入-输出特性由三阶表达式建模时,由线性项和二阶和三阶非线性产生的频率分量。
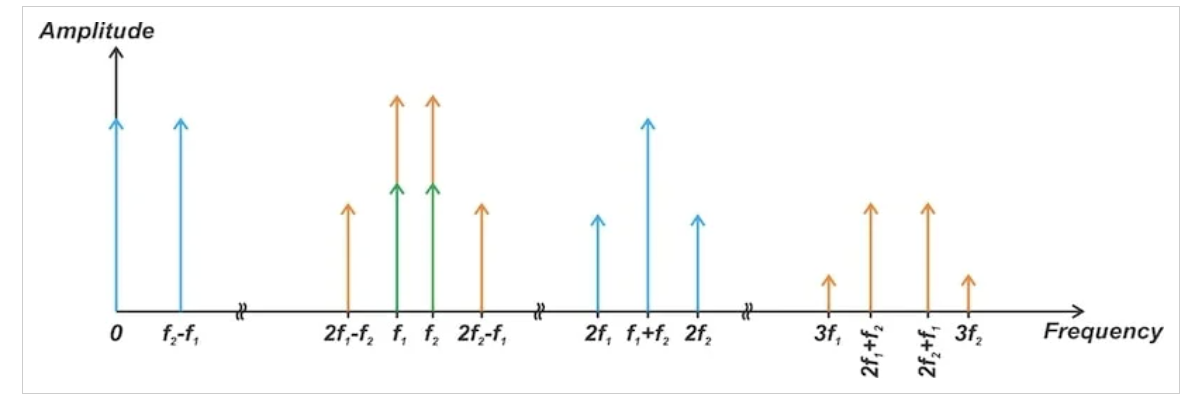 图2 当输入输出特性由三阶表达式建模时,由线性项(绿色)、二阶项(蓝色)和三阶项(橙色)产生的频率分量
图2 当输入输出特性由三阶表达式建模时,由线性项(绿色)、二阶项(蓝色)和三阶项(橙色)产生的频率分量请注意,该图没有描述组件的相对大小,只是描述了它们的存在和出现的频率。取决于电路非线性特性的相对幅度在这里并不重要。
接下来,让我们考虑两个非线性阶段的级联(图3)。
两个非线性阶段的级联。
 图3 两个非线性阶段的级联
图3 两个非线性阶段的级联通过双音输入,第一级在节点a处生成图2所示的所有频率分量。这些频率分量经历了第二级的非线性,并在节点B处生成了最终的失真分量。我们的目标是确定节点B处出现的整体IM3分量。
第一级产生的几个不同的失真分量可能会对级联输出端的IM3分量产生影响。例如,图2显示,由于其二阶非线性,第一级在2°2处产生失真分量。然后,由于第二级的二阶失真,该分量在⍵1处与基波分量混合,产生2 9077 2-9077》1处的互调(IM)产物。
然而,应该注意的是,2⍵2处的失真分量远离输入频率(9077 1和9077》2)。由于大多数射频电路的带宽很窄,我们预计2⍵2的组件会受到电路频率响应的严重抑制。因此,级联系统的简化非线性分析仅考虑输入频率附近的失真分量。
考虑到这一点,让我们研究一下产生输出IM3失真的两种混合机制。
第一阶段的三阶非线性
让我们从第一阶段产生的三阶失真开始。这与第二级的线性响应相结合,在输出端产生IM3分量。相关频率分量如图4所示。
第二级放大由第一级产生的三阶失真。
 图4 第二级放大由第一级产生的三阶失真
图4 第二级放大由第一级产生的三阶失真在上图中,我们看到第一级的三阶非线性在节点A处的频率2⍵1-ᮥ2和2⍴2-F 1处产生IM分量。第二级放大了这些失真项。
我们应用方程式4来计算节点A处IM分量的功率,得到:
 方程式6
方程式6其中OIP1是第一级的输出三阶截距点,PF,A是节点A处的基本输出功率。PF,A等于输入功率(P1)乘以第一级的增益(G1):
 方程式7
方程式7结合前两个方程,我们得到:
 方程式8
方程式8节点A处的IM功率乘以第二级(G2)的增益,并在输出端显示为:
 方程式9
方程式9上述方程式确定了第一机构对输出IM3功率的贡献。
第二阶段的三阶非线性
第一级的线性增益在第二级的输入端(节点A)产生基波分量。由于第二级的三阶非线性,它们在输出端(节点B)产生三阶IM分量。从方程7中我们知道,节点A处的基本分量具有P1G1的幂。因此,第二阶段通过双音测试进行激励,其中每个音调的功率为P1G1。如图5所示。
第一级放大输入分量,第二级产生三阶失真分量。
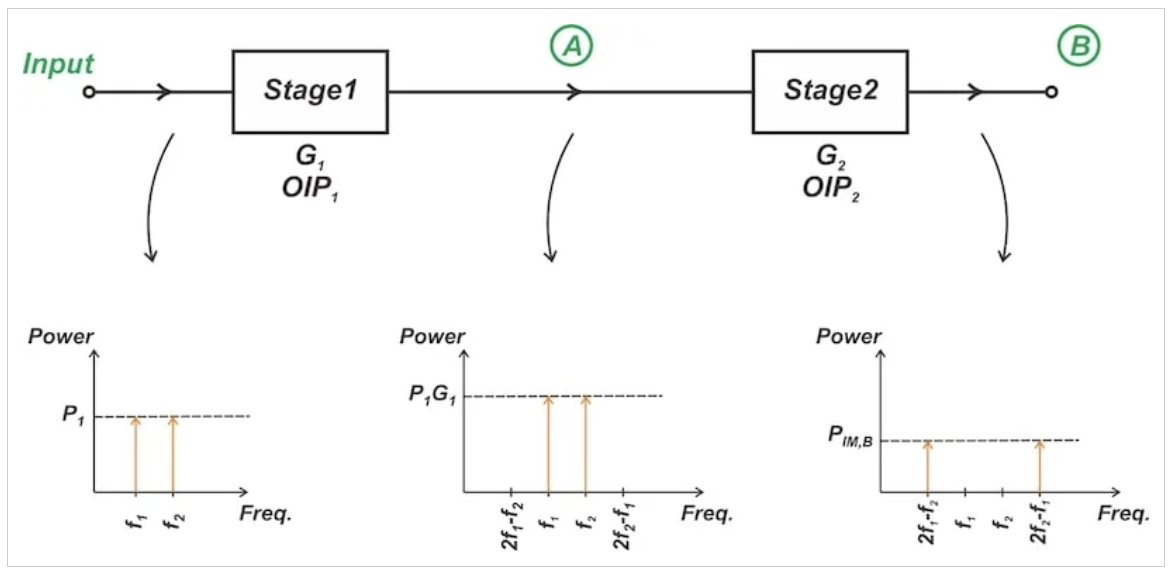 图5 第一级放大输入分量,第二级产生三阶失真分量
图5 第一级放大输入分量,第二级产生三阶失真分量将方程式4应用于第二阶段,我们得到:
 方程式10
方程式10在上述方程中,OIP2是第二级的输出三阶截距点,PF,B是节点B处的基本输出功率。PF,B等于第二级(P1G1)的基本功率输入乘以第二级
 方程式11
方程式11这是第二种机制对输出IM3功率的贡献。
畸变项的相干相加
在前面的章节中,我们计算了每个阶段对输出IM3分量的功率贡献。相关的问题是:这些组成部分是如何组合在一起产生输出IM3失真的?
由于互调信号是确定的,我们不能简单地增加功率。相反,我们必须处理电压。我们遵循三个步骤:
将电源组件转换为电压。
将电压相加,得出总失真电压。
将结果转换回电量。
来自第一机制的功率(方程式9)产生以下失真电压:
 方程式12
方程式12其中Z0是系统阻抗。类似地,来自第二机制的功率(方程式11)产生由下式给出的失真电压:
 方程式13
方程式13在最坏的情况下,V1和V2是同相的,加在一起产生输出IM3电压:
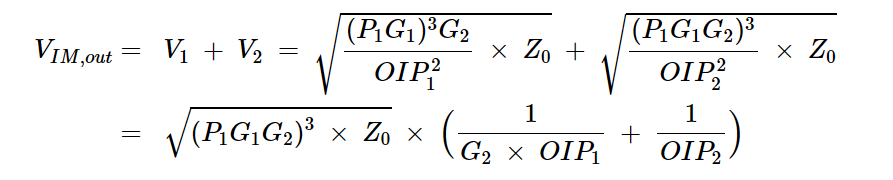 方程式14
方程式14我们取VIM的平方,将结果除以Z0,得到总输出IM3功率:
 方程式15
方程式15请注意,第一个括号内的项等于级联输出端的基本功率。用PF表示这个项,out,我们可以把上面的方程改写为:
 方程式16
方程式16该方程给出了级联输出端的IM3功率。通过注意其与描述单级输出端IM3功率的方程4的相似性,我们可以建立级联有效输出截点(OIPcas)的方程:
 方程式17
方程式17三级叶栅的截断点
现在我们已经研究了两级级联的非线性,让我们考虑一个三级级联系统(图6)。
三级级联。
 图6 三级级联
图6 三级级联我们使用与之前类似的程序获得三级级联的输出截距点:
 方程式18
方程式18请注意,分母项只是指整个系统输出的每个阶段的截距点。这意味着每个阶段的截距点乘以该阶段之后的总增益。如果后续阶段的总增益相对较大,则与该阶段相关的分数相对较小。因此,当增益项很大时,级联最后阶段的非线性变得越来越关键。
通过注意前一级的信号放大意味着后一级需要处理相对较大的信号,可以直观地理解这一点。这些较大的信号推动级联中的后期进入更非线性的操作区域。关键的结论是,当各阶段的增益显著时,后期阶段存在的任何非线性都会对整体系统性能产生更明显的影响。
示例:计算两级叶栅的三阶截点
为了巩固我们所学到的知识,让我们通过一个示例问题来解决。图7显示了一个输出截距为+8 dBm、增益为13 dB的低噪声放大器,后面是一个输入截距为0 dBm、增益10 dB的混频器。
包括LNA和混频器的级联系统的示例。
 图7 包括LNA和混频器的级联系统的示例
图7 包括LNA和混频器的级联系统的示例确定此系统的以下内容:
级联的输出截断点。
级联的输入截断点。
哪个阶段限制了级联的拦截点。
为了应用级联截距方程(方程17),我们首先将混频器截距点的参考从输入转移到输出:
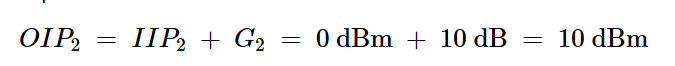 方程式19
方程式19然后,我们将分贝值转换为线性值:
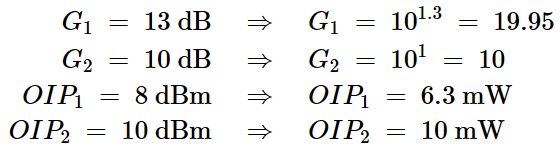 方程式20
方程式20将这些值代入方程17,我们得到级联的输出截距点:
 方程式21
方程式21根据方程式21,级联的输出截距点计算为OIPcas=8.63 mW=9.4 dBm。级联的输入截距点等于输出截距点减去总增益(以分贝为单位),从而得到9.4 dBm–(13+10)dB=–13.6 dBm的输入截隙点。
为了确定哪个阶段限制了级联的截断点,让我们假设混频器具有完美的线性(OIP2=无穷大)。从级联截距方程中,我们观察到,当OIP2接近无穷大时,系统的输出截距点变为OIPcas=OIP1G2。在这种情况下,使用分贝单位,OIPcas的计算结果为8 dBm+10 dB=18 dBm。
这远远大于混频器的输出截距点,即10dBm。因此,混频器限制了级联的线性度。为了验证这一点,我们注意到计算出的输出截距点为OIPcas=9.4 dBm。该量接近混频器的输出截距点(OIP2=10dBm)。
总结
实用的射频系统由几个不同模块的级联组成。在这篇文章中,我们讨论了各个组成级的线性度如何影响整个级联的线性性能。当级具有显著增益时,后期级中存在的任何非线性都会更深刻地影响整体系统性能。因此,在最后阶段仔细管理和理解非线性至关重要,尤其是在处理实质性收益时。
<!-- 非定向300*250按钮 17/09 wenjing begin --> <!-- 非定向300*250按钮 end -->
</div>

