背景
密态计算能够支持多方联合建模而不泄漏数据价值。该方案是基于蚂蚁密算隐语团队开发的 Secret Sharing - Generalized Linear Model (SS-GLM) 算法完成了联合建模的步骤。
很多业务小伙伴们多次询问我们是否可以进一步提升该算法的性能。
通过分析 SS-GLM 算法的性能，我们发现 exp 算子占用了40%以上的计算时间，高于其他任何单一操作。
根据德摩根定律，如果能够改进 exp 算子，将会带来最大的性能提升。此外，exp 算子广泛应用于机器学习模型中的激活函数，甚至在大型模型如 Transformer 中也有大量的 exp 计算。
过去的方法往往牺牲精度，或者为特定模型提供特定的启发式算子来提高性能。虽然这些方法在少数场景中可以获得显著提升，但其影响力和适用范围较为有限。尽管难度高，改进 exp 算子收益太大了，必须要迎难而上。
通过我们的研究，发现在 exp prime 方向上的算法工作具有理论实现的可能性，并且有潜在的巨大收益。
因此，我们团队决定将其适配到SPU 的 SEMI2K[1] 协议中。
我们实现了新版的 exp 计算方法，称为 exp prime[2]。
然而，由于理论细节非常复杂，我们的改进在算法理论和工程实现上都进行了大量的微创新，因此我们无法直接预测 exp prime 在实际业务中的表现，特别是不确定它的精度和稳定性（是否能在较大范围内完成高精度计算）。评估密态算子的性能本身非常困难。
MPC (Secure Multi Party Computation 多方安全计算) 算子设计需要多方通信和复杂的密码学交互，并且受网络条件的影响很大。
目前 SPU 的 MPC 算子基于定点数实现，因此新算子的精度是否能达到业务需求仍是未知数。
开发一个新的算子，特别是基于复杂理论和工程实践的算子，业务团队能否放心使用，计算时间能否减少，内存消耗是否会增加，模型精度是否会受到影响，适配新算法能否带来显著收益，投资回报率是否高，这些都是难以回答的问题。
与我们长期合作的业务团队尚且对密态算子的性能缺乏直观感受，而对密态计算感兴趣的潜在合作方可能对这种性能评估更加陌生。
因此，本文系统地评估了 exp 算子的性能，旨在为当前的业务方和未来的合作方提供参考。本文的测评方法[3]将全部开源，以确保结果的可复现性。
测评定义
根据 MPC 算子的计算模式，以下维度能够影响算子执行的耗时和消耗的资源，以及效果：
- 通讯量
- 轮数
- 内存
- 有效模拟范围
- 误差大小
- 耗时
在固定场景 SEMI2K FM128 下进行测试，因为 exp prime 目前仅支持该场景。
我们选择了在 SPU 中现有的所有 exp 方法进行比较：
- exp pade 方法：初版高精度的 exp 模拟方法，强制启用了下限和上限的 clamping。代号为 mod 1。
- exp taylor 方法：基于泰勒级数的模拟方法，可以通过调节迭代次数控制精度。迭代次数越多，性能越差。本次测试使用泰勒-8参数。预期性能大大优于 pade 方法，但精度较差，没有 clamping。代号为 mod 2。
- exp prime 方法：最新实现的 exp 计算方法，clamping 可配置，默认启用下限 clamping。代号为 mod 3。
注：
- clamping 指的是限制输入数值的范围。例如，合适的范围为 [-10, 10]，那么输入为-100时，我们将其处理为-10。
- clamping 在密态计算中开销很大，应尽量避免。
- clamping 设置为一般训练时能跑通的最快设置（经验设置）。
结果前瞻
exp prime 能力六个测评维度上，都有优势，属于硬核突破。exp prime 在任何维度对于原有方法都具有优势。
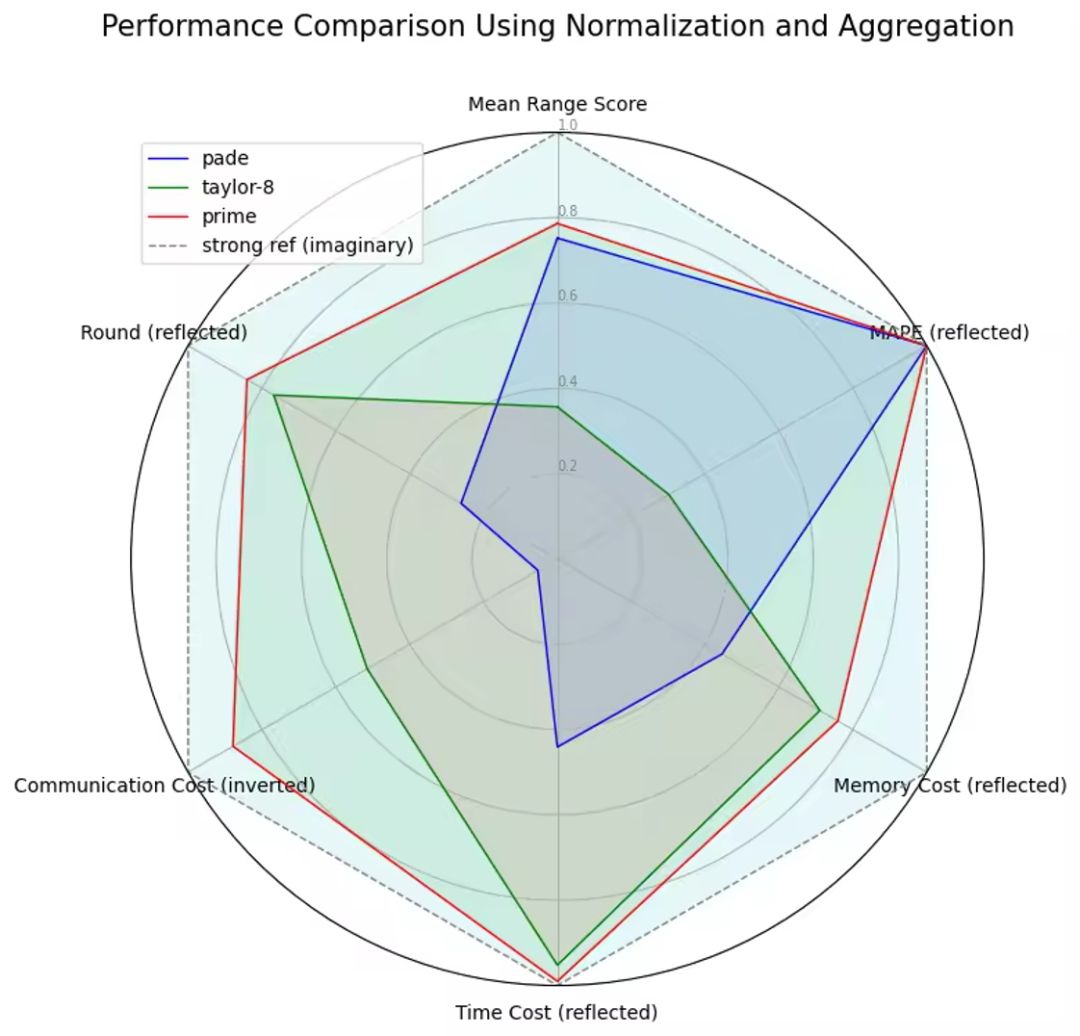
各维度分析
1. 通讯量
MPC 算子网络性能的首要考虑因素。在实际业务落地中，MPC 算子的最大瓶颈在于带宽需求。
由于计算过程中需要大量通信，增加 CPU 数量和性能并不能有效地减少计算耗时，而提升带宽则可以。
提升带宽的问题则在于，一般的业务场景下，带宽并不像购买 CPU 那样容易提升。因此，在其他条件不变的情况下，MPC算子的通讯量越低，其计算耗时越短，且带宽越小，这种效应就越明显。
假设x为n个元素的数组，则exp(x)消耗的通讯量为平均通讯量乘以n。传输耗时与通讯量成反比。
例子：a, b, c 为 SEMI2K 下被秘密分享的3个数字。假如 pade 模式下 exp([a, b, c]) 消耗的通讯量为 1208 * 3 = 3624 bytes。假设带宽为 每秒1024 bytes，那么，不考虑其他计算，单单传输上述通讯量需要 3624/1024 = 3.54s。
结果
| exp mod | 平均通讯量 bytes |
|---|---|
| pade | 1208 |
| taylor-8 | 272 |
| prime | 169 |
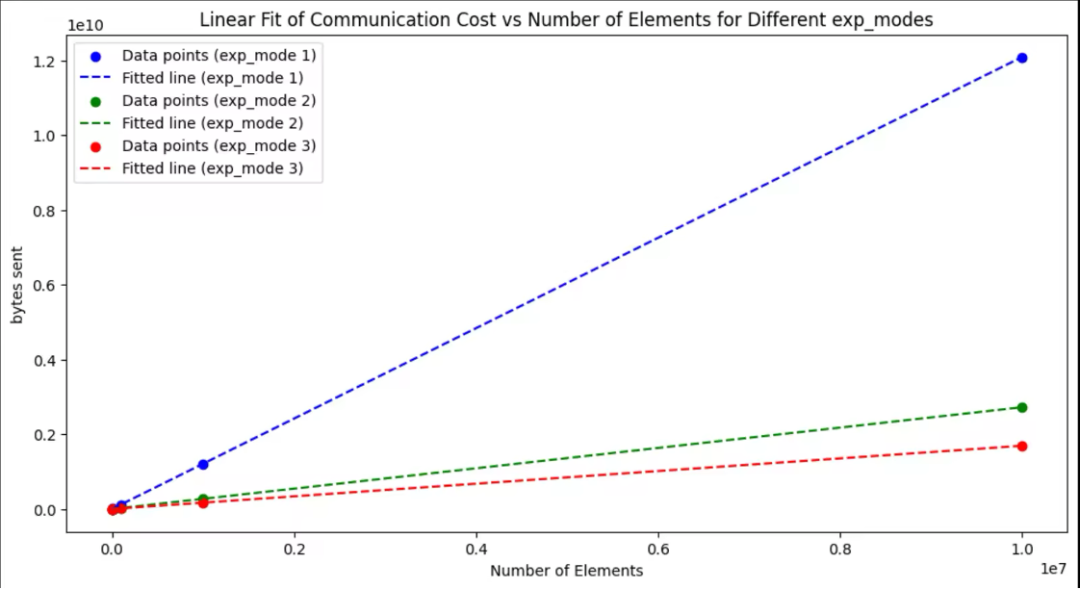
数据 – exp 通讯量和轮数测量结果
num_elements,exp_mode,bytes_sent,round
10,1,12080,52
10,2,2720,17
10,3,1690,12
100,1,120800,52
100,2,27200,17
100,3,16900,12
1000,1,1208000,52
1000,2,272000,17
1000,3,169000,12
10000,1,12080000,52
10000,2,2720000,17
10000,3,1690000,12
100000,1,120800000,52
100000,2,27200000,17
100000,3,16900000,12
1000000,1,1208000000,52
1000000,2,272000000,17
1000000,3,169000000,12
10000000,1,12080000000,52
10000000,2,2720000000,17
10000000,3,1690000000,12
小结
exp prime （单方clip）通讯量比高精度pade 方法低7倍，为taylor-8方法的2/3， 是当前通讯量消耗最低的SEMI2K exp计算方法。网络条件越恶劣，exp prime 优势越大。
2. 轮数
MPC 算子网络性能的次要因素。MPC 算子实现一次计算通常需要多次交互，如果网络延迟高，则轮数越高的算子受延迟影响越大。
若网络延迟为 10ms，exp(x) 通讯的轮数为 r。受延迟影响的传输耗时为 10r ms。但是不论 exp 要计算的元素数据量有多大，轮数是固定的。
结果
| exp mod | 轮数 |
|---|---|
| pade | 52 |
| taylor-8 | 17 |
| prime | 12 |
小结
exp prime （单方clip）通讯轮数比高精度pade 方法低4倍，为taylor-8方法的2/3， 是当前轮数消耗最低的SEMI2K exp计算方法。网络条件越恶劣，exp prime 优势越大。
3. 内存
计算数据时候存在内存消耗， 如果最大内存（Peak Memory） 超过了计算机的 RAM, 则会报错终止进程。
我们对于内存消耗建模为 y = a n+ b；y 为内存峰值，n 为需要计算的元素数量，a 为平均一个元素的内存消耗，b 为程序与元素数量无关的内存开销。
结果
| exp mod | 平均内存消耗（kb） | 其他内存开销(kb) |
|---|---|---|
| pade | 0.1 | 191083 |
| taylor-8 | 0.1 | 185784 |
| prime | 0.1 | 184807 |
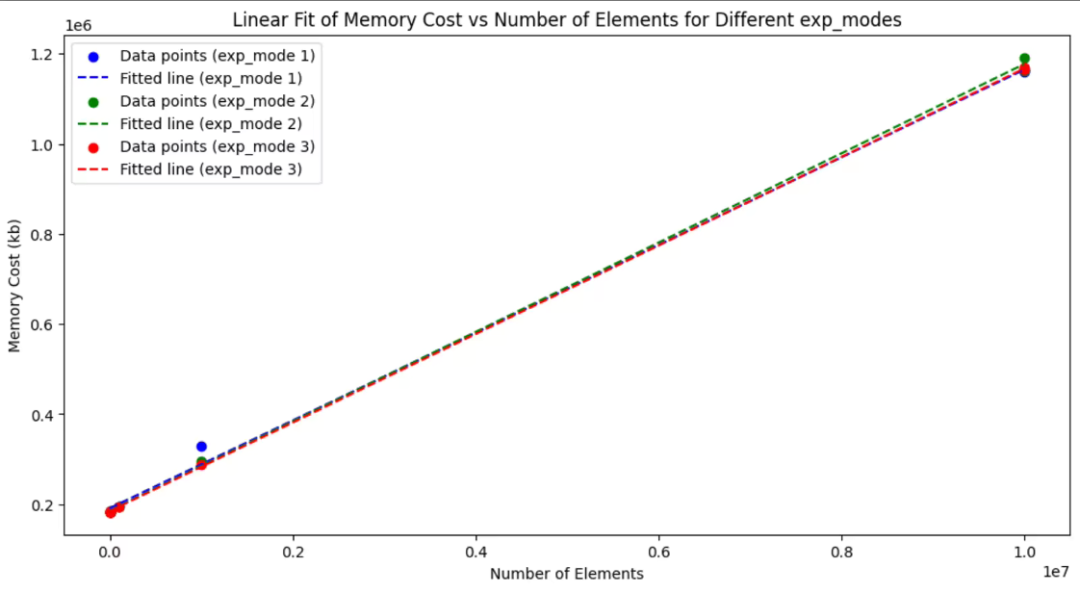
数据 – exp 内存消耗测量结果
num_elements,exp_mode,mem_cost(kb)
10,1,183296
10,2,183808
10,3,183808
100,1,183296
100,2,183808
100,3,183808
1000,1,183296
1000,2,183808
1000,3,183296
10000,1,183808
10000,2,184832
10000,3,184320
100000,1,195756
100000,2,194716
100000,3,194968
1000000,1,329248
1000000,2,294868
1000000,3,288316
10000000,1,1160468
10000000,2,1161496
10000000,3,1168996
10000000,1,1164852
10000000,2,1191800
10000000,3,1164632
小结
exp prime 边际内存消耗和pade， taylor 相当， 总消耗不高于前两种方法。
4. 有效模拟范围
MPC 下的 exponential 算子和明文相比有差距。若 exp(x) MPC 计算的模拟误差和明文差距不大，则在 MPC 下计算 exp(x) 是有实际意义的，若误差过大比如则不能视为有效的模拟计算。
如果告诉你一个算法，速度很快，精度很高，但是它要求输入必须是[-10, 10]之间的数字，那么它是一个好算法吗？如果输入范围以外的数字，答案会错得离谱。
例如，业务场景下输入的数字范围是[-10, 30]怎么办？业务大概率不能使用这个算法。有效范围越大，可运用的业务范围就越广，场景就越多。
默认参数下的有效模拟范围：
对于 [-40,40] 中等距采样10000个数，精准模拟的数 / 10000 = 精准模拟的比例。
精准模拟的标准：
绝对误差 Absolute Error = |x_true – x|
相对误差 Absolute Percentage Error : |x_true – x| / |x_true|
下表中AE < 5 的含义是 绝对误差< 5 视作精准模拟。下表中的数值为精准模拟比例，明文参考值为1。
结果
exp prime 平均有效模拟比例为0.629， 在长度为[-40, 40]的范围内能有效模拟接近2/3的数值。有效范围高于exp pade 方法，大大高于taylor-8方法。
但是一旦不在有效模拟范围，无clamping exp prime 的误差也许会大到离谱。
数据
| exp mode | ape < 5% | ape < 1% | ape < 0.05% | ae < 5 | ae < 1 | ae < 0.05 | mean range score |
|---|---|---|---|---|---|---|---|
| prime | 0.6177 | 0.5981 | 0.5607 | 0.7074 | 0.6925 | 0.6561 | 0.629 |
| taylor-8 | 0.1285 | 0.0568 | 0.0126 | 0.5595 | 0.5458 | 0.5242 | 0.285 |
| pade | 0.5557 | 0.5548 | 0.5439 | 0.6811 | 0.6624 | 0.626 | 0.602 |
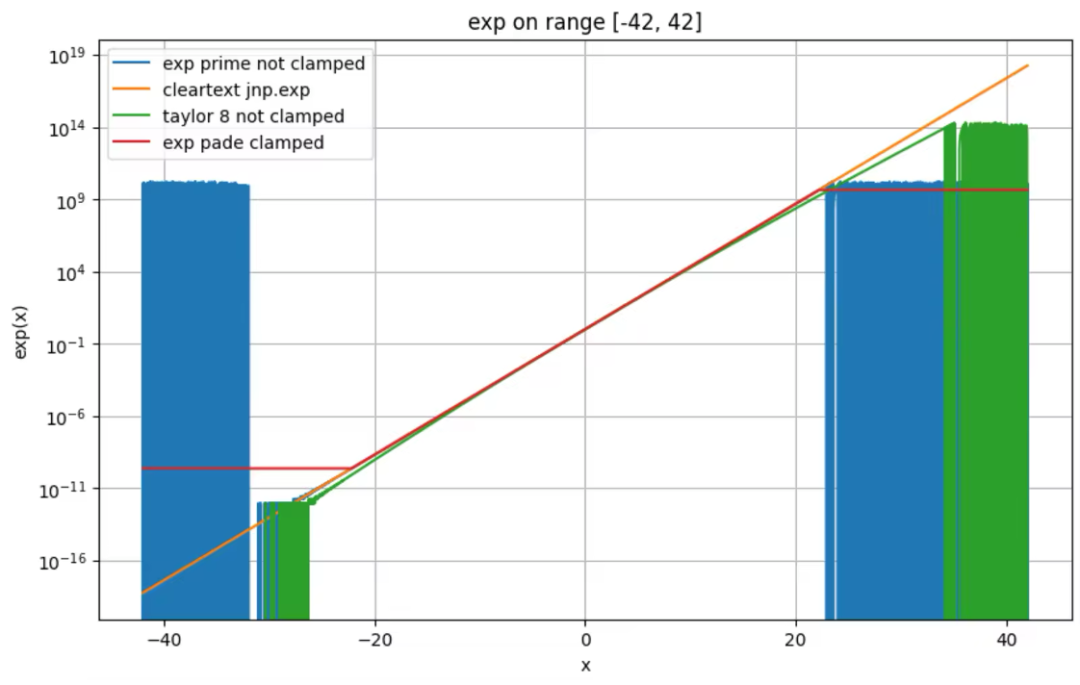
一旦不在有效模拟范围，无 clamping exp prime 的误差也许会大到离谱。根据该结果，我们在工程实践中使用了可配置的 clamping, 本文所有测评都是基于默认参数启用lower clamping 完成的 （因为常用输入总是超过下界，而不超过上界）。
taylor-8 看起来模拟范围更大？其问题是表面看起来差距不大，但是实际误差已经很大了（上图为 log scale）。上图中 taylor-8, ape < 5% 的范围可能比肉眼感觉的要小的多。
通过下图 exp 和明文的误差来演示这一点，注意 y轴 为 10^6 。
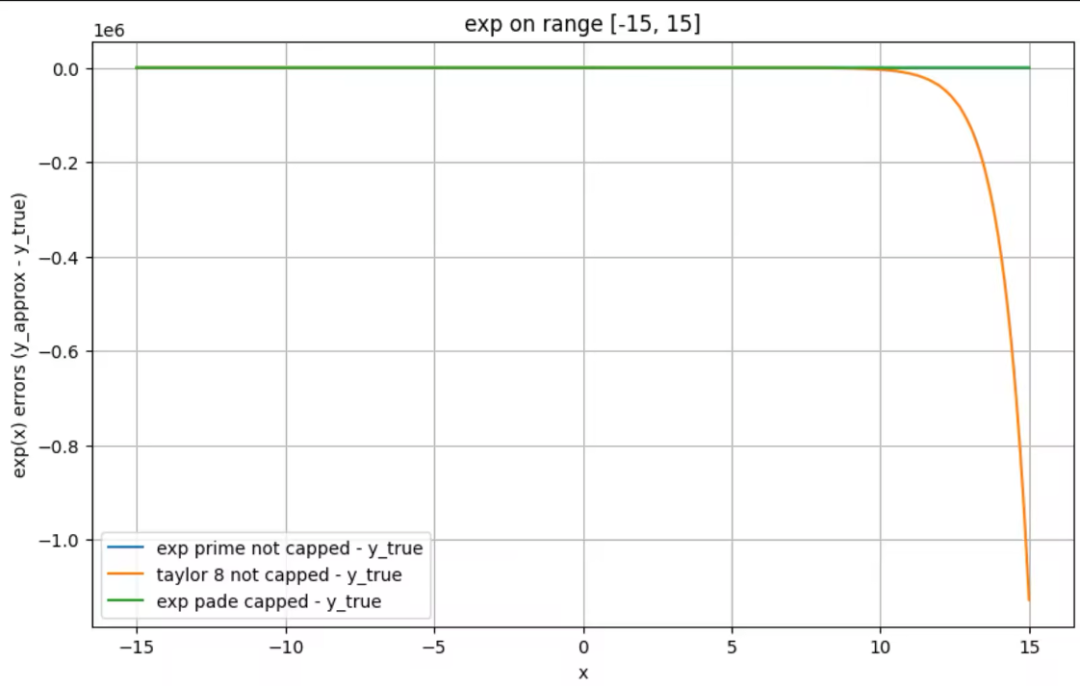
小结
exp prime 使用场景大概率广于pade和taylor-8 算法，如果过去taylor和pade方法能满足需求，则可以放心使用exp prime 方法。
大部分场景下使用默认参数即可，输入过大时需要启用upper clamping。
5. 误差大小
即使所有计算都在常用且能够有效模拟的范围内进行，我们仍然希望 exp 计算的误差尽可能低，以接近明文计算的精度。
在离线 MPC 训练和在线联邦预测的场景下，在线预测使用的是明文计算的 exp。如果误差较大，那么在线预测与离线训练之间的差异也会随之增大。
想象一下，在一个二分类场景中，你训练了一个AUC达0.97的模型，为了将AUC从0.94提升到0.97，你花费了大量精力进行优化（离线预测测试）。
然而，仅仅是训练和预测之间的exp计算误差就可能使在线预测的AUC降到0.965。更糟糕的是，你本可以达到0.98的AUC，但由于MPC exp计算误差，你只能达到0.97的AUC。
精度误差可以导致AUC下降0.025！这正是使用MPC建模的算法工程师在联合建模效果上的一大困扰。因此，我们一定希望exp计算的误差越低越好！
结果
exp prime 的平均绝对误差， 平均相对误差，平均误差平方都是现有方法中最低的。比过去高精度的方法精度要高1-3个数量级。
数据
在x 为[-20, 20] 的数字中我们比较 exp模拟的 Mean Squared Error， Mean Absolute Error 和 Mean Absolute Percentage Error
| exp mode | mse | mae | mape |
|---|---|---|---|
| prime | 1075.37 | 6.12 | 3.898e-06 |
| taylor-8 | 759747514271408.9 | 5943857.74 | 0.209 |
| pade | 1322195.69 | 153.83 | 1.605e-05 |
小结
exp prime 的精度最高，十分接近明文，能满足绝大部分场景的精度需要，远超过去方法。
6. 耗时
计算耗时是算法工程师、业务方都高度关注的一个指标，也是过去性能benchmark中唯一各方关注的指标，打榜就靠它了。
- 对于算法工程师来说，如果跑一个联合建模算法要8小时，一条只能调参1次，如果联合建模耗时5小时，那么一天能够调参2次，效率提高1倍。
- 对于业务来说，以前更新一次数据，完全新的联合建模要15天，现在如果能10天上线，那么提早5天上线，多创造的这部分价值就是收益。可以想象一下，若有几十个机构，平均每半年就要更新一次更新数据联合建模，服务数亿级别的客户，降低耗时创造的价值是巨大的。
但是，MPC 场景的耗时测量受很大的网络参数影响。LAN 网络下，所有 MPC 计算好像都挺快，WAN 网络下，MPC 计算耗时能长到令人怀疑人生。
我们采取以下场景进行耗时评测：
net level specification
-
net_rate=”100000mbit” net_latency=”0ms”;;
-
net_rate=”1000mbit” net_latency=”1ms”;;
-
net_rate=”100mbit” net_latency=”10ms”;;
-
net_rate=”10mbit” net_latency=”100ms”;;
我们对于时间消耗建模 为 y = a n+ b，y 为耗时，n 为需要计算的元素数量，a 为平均一个元素的时间消耗 （边际耗时），b 为程序与元素数量无关的时间开销。
结果
net level 2，100Mb 带宽，10ms 延时，是一个最常用的评测场景。
| exp mod | net_level 2 边际耗时（s） |
|---|---|
| pade | 12.065e-05 |
| taylor-8 | 2.86e-05 |
| prime | 2.18e-05 |
其他耗时可参考下图
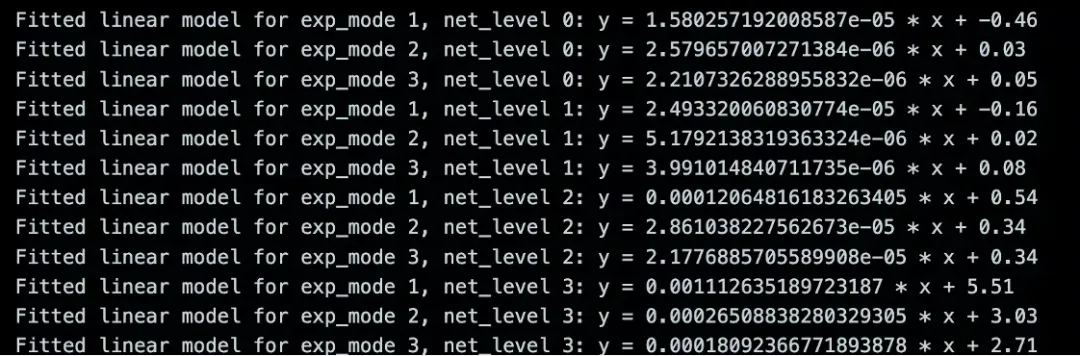
数据 – exp 时间消耗测量结果
num_elements,exp_mode,elapsed_time,net_level
10000,3,0.10899242595769465,0
100000,1,1.5562007201369852,0
100000,2,0.3806668110191822,0
100000,3,0.36923978198319674,0
1000000,1,12.413455325877294,0
1000000,2,2.3289378818590194,0
1000000,3,2.0647744049783796,0
10000000,1,157.84879399999045,0
10000000,2,25.858311526011676,0
10000000,3,22.179473932133988,0
10,1,0.13805793807841837,1
10,2,0.09943982097320259,1
10,3,0.10655678412877023,1
100,1,0.15299400803633034,1
100,2,0.10206696693785489,1
100,3,0.09619212592951953,1
1000,1,0.17369073489680886,1
1000,2,0.11150461691431701,1
1000,3,0.10390148684382439,1
10000,1,0.3839655520860106,1
10000,2,0.1682215000037104,1
10000,3,0.17196061299182475,1
100000,1,2.7040774549823254,1
100000,2,0.6501772250048816,1
100000,3,0.5786988700274378,1
1000000,1,23.041077816160396,1
1000000,2,4.713096359046176,1
1000000,3,3.8042779518291354,1
10000000,1,249.34486315306276,1
10000000,2,51.86276936996728,1
10000000,3,40.010631297016516,1
10,1,0.7347624329850078,2
10,2,0.3620553209912032,2
10,3,0.335803555091843,2
100,1,0.7282703381497413,2
100,2,0.3660985380411148,2
100,3,0.3254895710851997,2
1000,1,0.8166786769870669,2
1000,2,0.441350911045447,2
1000,3,0.3981817150488496,2
10000,1,1.6240983819589019,2
10000,2,0.6257592940237373,2
10000,3,0.5846053399145603,2
100000,1,12.155489874072373,2
100000,2,3.043655260000378,2
100000,3,2.4608653138857335,2
1000000,1,121.23415710008703,2
1000000,2,28.960522881010547,2
1000000,3,22.12015020288527,2
10,1,6.521644555963576,3
10,2,2.888359455158934,3
10,3,2.4858575160615146,3
100,1,6.515798039967194,3
100,2,2.910730817820877,3
100,3,2.4944541668519378,3
1000,1,7.144702007062733,3
1000,2,3.7519471780397,3
1000,3,3.115263829007745,3
10000,1,13.943796247942373,3
10000,2,5.395836747949943,3
10000,3,4.7630465012043715,3
100000,1,117.0330176721327,3
100000,2,29.69434425421059,3
100000,3,20.770910662133247,3
1000000,2,268.1107207580935,3
小结
exp prime 边际耗时在所有场景下都是最低的，且网络条件越恶劣，相对优势越大。应证了之前根据网络条件的推理。
总体分析
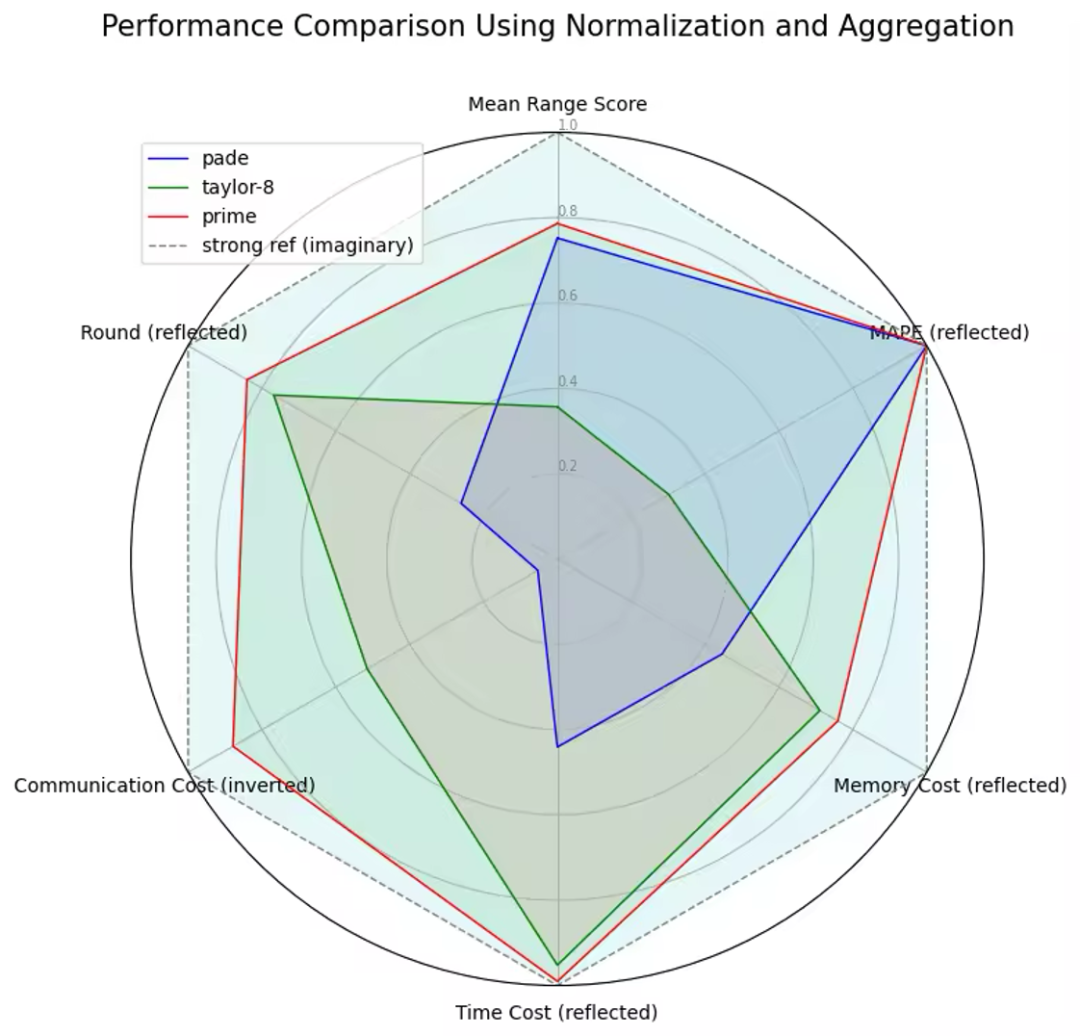
各个维度上，exp prime 都是目前最优的指数计算方法。
我们选取了各个维度的指标，并进行了转换处理，以可视化其相对优势。具体而言：
- 通讯量：采用 ( 1/边际通讯量 ) 的标准来打分，通讯量越高分数越低。
- 轮数：采用（-轮数）的标准来打分，轮数越低分数越高。
- 有效模拟范围：采用平均有效比例的标准来打分，平均有效比例越高分数越高。
- 误差大小：采用 (-MAPE) 的标准来打分，MAPE越高分数越低。
- 内存：采用 (-边际内存消耗}) 的标准来打分，边际内存消耗越高分数越低。
- 耗时：采用 (-net_level 2 边际耗时) 的标准来打分，边际耗时越高分数越低。
总结
exp prime 新方法在各方面的模拟计算性能均优于之前的方法，适用范围更广，效果更好，耗时更低，同时保持了相同的安全性。
在不做任何妥协的情况下，exp prime 显著提升了 exp 的性能，精度和有效模拟范围也大大超出了预期。
作为一个基础算子，exponential 在众多算法中都扮演着重要角色。无论是树模型还是线性模型，无论是联合分析还是 MPC 大模型训练，只要算法中使用了 exp prime，都能获得显著的性能提升和表现改善，预计将创造巨大的价值。
复现
exp prime 方法已经递交了专利，且相应代码已经开源，暂时实验性地支持了 SEMI2K FM128 场景。
[1] SPU SEMI2K 协议：（欢迎 star 🌟 ，关注更多技术更新动态～
https://github.com/secretflow/spu/blob/main/src/libspu/mpc/semi2k
[2] exp prime 方法代码：
https://github.com/secretflow/spu/blob/main/libspu/mpc/semi2k/exp.h
[3] 测评思路：具体流程 — 起 Docker、限制带宽、RUN、收集数据、分析
https://github.com/secretflow/spu/tree/atc23_ae
参考
该方法参考了以下论文进行改造实现：
- 《Secure Poisson Regression》：https://www.usenix.org/system/files/sec22summer_kelkar.pdf
- 《A Framework for Secure Two-Party Computation through Efficient Modulus Conversion and Mixed-Mode Protocols》 (no publication yet)
</div>
